The Two Egg Problem

There’s an interesting mind-teaser/puzzle that floats around the internet in waves. Sometimes it’s described as a Google interview question; sometimes it’s described as a Microsoft interview question. No matter of the origin, it’s a fun little critical thinking puzzle and in this blog posting I’m going to look into it and take it a little further …

Puzzle Definition

You are given two eggs, and access to a 100-storey building. Both eggs are identical. The aim is to find out the highest floor from which an egg will not break when dropped out of a window from that floor. If an egg is dropped and does not break, it is undamaged and can be dropped again. However, once an egg is broken, that’s it for that egg.

If an egg breaks when dropped from floor n, then it would also have broken from any floor above that. If an egg survives a fall, then it will survive any fall shorter than that.

The question is: What strategy should you adopt to minimize the number egg drops it takes to find the solution?. (And what is the worst case for the number of drops it will take?)

There are no tricks, gotchas or other devious ruses. Don’t rat-hole with issues related to terminal velocity, potential energy or wind resistance. This is a math puzzle plain and simple.

Think about the puzzle for a few minutes, and then read on.

有一栋100层高的大楼，给你两个完全相同的玻璃球。假设从某一层开始，丢下玻璃球会摔碎。那么怎么利用手中的两个球，用什么最优策略知道这个临界的层是第几层？

One Egg

Whilst it’s not strictly part of the puzzle, let’s first imagine what we’d do if we had only one egg.

Once this egg is broken, that’s it, no more egg. So, we really have no other choice but to start at floor 1. If it survives, great, we go up to floor 2 and try again, then floor 3 … all the way up the building; one floor at a time. Eventually the egg will break* and we’ll have a solution. For example, if it breaks on floor 57, we know that the highest floor that an egg can withstand a drop from is floor 56.

There’s no other one egg solution. Sure, if we’d been feeling lucky we could have gone up the floors in two’s but imagine if the egg broke on floor 16; we have no way of knowing if it would have also broken on floor 15!

Many Eggs

At the other extreme, what if we had an infinite number of eggs? (Or at least as many eggs as we need). What would our strategy be here? In this case we’d use one of a programmer’s favorite tools, the binary tree.

First we’d go to floor 50 and drop an egg. It either breaks, or it does not. The outcome of this drop instantly cuts our problem in half. If it breaks, we know the solution lives in the bottom half of the building (floor 1 – floor 49). If it survives, we know the solution is in the top half of the building (floor 51 – 100). On each drop, we keep dividing the problem in half and half again until we get to our solution.

The mathematicians in the audience will quickly see that the number of drops required for this solution is log2 n, where n is the number of floors of the building. (This is like asking how many powers of two there are).

Because this building does not have a number of floors equal to a round number power of two, we need to round up to number of drops to get seven ( log2 100 = 6.644 )

(Using seven drops, we could solve this problem any building up to 128 floors. Eight drops would allow us to solve the puzzle for a building with twice the height at 256 floors …)

Depending on the final answer, the actual number of eggs broken using a binary search will vary. At worst it will be seven eggs (if the floor is actually floor 1, since every drop will break the egg). At best it will be no eggs (if the actually answer is floor 100, since the egg will survive every drop made).

(There’s a very interesting lesson here which I’ll cover in a future posting: Understanding the difference between Expected Answer and Worst Case Answer. These can be very different things!)

Back to two eggs

OK, let’s get back to the original two egg problem. As we’ve seen from above, the worst case using a binary search would break seven eggs; not acceptable when we only have two eggs.

It does not take much imagination to see why a binary search solution will not work (optimally) for two eggs. Let’s imagine we did try a binary search and dropped our first egg from floor 50. If it broke, we’d be instantly reduced to a one egg problem, so then we would have to start with our last egg from floor 1 and keep going up one floor at a time until that breaks. As a worst case, it will take us 50 drops. We can do better …

What happens if we started off with our first egg going up by floors ten at a time? We can start dropping our egg from floor 10; if it survives we try floor 20, then floor 30 … we carry on until the first egg breaks. Once we’ve broken our first egg we know that the solution must lay somewhere in the nine floors just below, so we back off nine floors and step through these floors one at a time until we find a solution.

This is certainly an improvement, but what is our worst case with this strategy? Well, imagine we dropped eggs on every 10th floor all the way up, and our first egg broke on floor 100. This has taken us ten drops so far. Now we know the solution must lay somewhere between floor 91 and floor 99 and we have to go through these in ones, starting at floor 91. The worst case would be if the solution was on floor 99, and this would take us nine more drops to determine. The worst case therefore, if we go by tens, is 19 drops.

Thinking about the 10 floor strategy again we can see that, whilst our worst case is 19 drops, some other possible solutions will take less than this (for instance, if the first egg broke on floor 10 then, at worst, from here we only have to make nine more drops to find the solution). Knowing that, what if we dropped our first egg from floor 11 instead? If the egg breaks on this floor, it will still only take ten more drops to find the solution (and if it doesn’t break, great, we’ve eliminated more floors than before! win-win?) Let’s follow this idea, and see where it leads …

Well, how about if we dropped our first egg from floor 12 then? A similar argument to above; if it breaks, we only have to try eleven floors with the second egg. If it doesn’t break, we can step up another dozen floors, and so on … But hold on a minute! … If first we try floor 12, then 24, then 36, then 48, 60, 72, 84, 96 then it finally breaks, we’ve wasted eight drops already, and we still have to check (up to) eleven more floors with our second egg, so we’re back at a worst case of 19 drops.

Problems where the solution lays lower down the building are taking less drops than when the solution lays higher up. We need to come up with a strategy that makes things more uniform.

Minimization of Maximum Regret

What we need is a solution that minimizes our maximum regret. The examples above hint towards what we need is a strategy that tries to make solutions to all possible answers the same depth (same number of drops). The way to reduce the worst case is to attempt to make all cases take the same number of drops.

As I hope you can see by now, if the solution lays somewhere in a floor low down, then we have extra-headroom when we need to step by singles, but, as we get higher up the building, we’ve already used drop chances to get there, so there we have less drops left when we have to switch to going floor-by-floor.

Let’s break out some algebra.

Imagine we drop our first egg from floor n, if it breaks, we can step through the previous (n-1) floors one-by-one.

If it doesn’t break, rather than jumping up another n floors, instead we should step up just (n-1) floors (because we have one less drop available if we have to switch to one-by-one floors), so the next floor we should try is floor n + (n-1)

Similarly, if this drop does not break, we next need to jump up to floor n + (n-1) + (n-2), then floor n + (n-1) + (n-2) + (n-3) …

We keep reducing the step by one each time we jump up, until that step-up is just one floor, and get the following equation for a 100 floor building:

n + (n-1) + (n-2) + (n-3) + (n-4) + … + 1  >=  100

This summation, as many will recognize, is the formula for triangular numbers (which kind of makes sense, since we’re reducing the step by one each drop we make) and can be simplified to:

n (n+1) / 2  >=  100 n（n+1） / 2 >= 100

This is a quadratic equation, with the positive root of 13.651 (Which we have to round up to 14. This is not a John Malkovich movie!).

Two egg solution

We now have all the information to compute the optimal two egg solution.

Our first drop should be from floor 14, if egg survives we step up 13 floors to floor 27, then up 12 floors to 39 …

The optimal strategy is to work our way through the table until the first egg breaks, then back up to one floor higher than the line above and then proceed floor-by-floor until we find the exact solution.

The maximum of 14 drops is a combination first egg drops (made in steps), and second egg drops (made in ones). For every drop we take hopping up the tower, we reduce the worst-case number of single drops we’d have to take so that no solution is an outlier.

Drop	Floor
#1	14
#2	27
#3	39
#4	50
#5	60
#6	69
#7	77
#8	84
#9	90
#10	95
#11	99
#12	100

Look see I can do three

Why stop at two eggs? What is the optimal strategy if we had three eggs? (Dare I say four? five? …)

Things get more complex with three eggs, but taking a deep breath we can apply the same principle of minimizing maximum regret. We need to select our first egg such that, if it breaks, or does not break, it results in a problem, which recursively is now a two egg problem, that we already know how to solve to minimize maximum regret!

Let’s define our building to have a maximum of k floors. Let’s say that the number of egg we have is represented by e, and the floor we are currently attempting to drop from is represented by n. With me so far? OK, what we need to find our optimal solution is to calculate what would happen if we dropped an egg from every floor (1 through to k) and (recursively) calculate the minimum number of droppings needed in the worst case. We’re looking for the floor that gives the minimum solution to the worst case.

If we drop an egg from floor n, one of two events happens:

1. The egg breaks, so now our problem is reduced to a tower of height n-1, and we now have e-1 eggs.
2. The egg doesn’t break and now we need to check k-n floors and we still have e eggs.

Remember we need to mimimize the number of drops in the worst case, so we take the higher (max) of these two situations, and select the floor which yields the minimum number of drops.

The code to solve this is fairly easy to write recursively, but suffers from a common problem that occurs with recursive solutions in which the same sub-problems are evaluated again, and again, and again, dragging performance to a grind for anything other than trivial solutions. To get around this, we need to keep track of values already computed so that we don’t have to repeat the calculation.

Rather than getting lost in gnarly code, let’s just share some of the results, and for some buildings higher than 100 stories.

Lots of of eggs, and lots of floors

Here’s a table showing the worst case number of drops it would take for a variety of floors with anywhere from 1 – 10 eggs.

	Eggs
Building Height	1	2	3	4	5	6	7	8	9	10
—	—	—	—	—	—	—	—	—	—	—
1 floor	1	1	1	1	1	1	1	1	1	1
2 floors	2	2	2	2	2	2	2	2	2	2
3 floors	3	2	2	2	2	2	2	2	2	2
4 floors	4	3	3	3	3	3	3	3	3	3
5 floors	5	3	3	3	3	3	3	3	3	3
6 floors	6	3	3	3	3	3	3	3	3	3
7 floors	7	4	3	3	3	3	3	3	3	3
8 floors	8	4	4	4	4	4	4	4	4	4
9 floors	9	4	4	4	4	4	4	4	4	4
10 floors	10	4	4	4	4	4	4	4	4	4
11 floors	11	5	4	4	4	4	4	4	4	4
12 floors	12	5	4	4	4	4	4	4	4	4
13 floors	13	5	4	4	4	4	4	4	4	4
14 floors	14	5	4	4	4	4	4	4	4	4
15 floors	15	5	5	4	4	4	4	4	4	4
16 floors	16	6	5	5	5	5	5	5	5	5
17 floors	17	6	5	5	5	5	5	5	5	5
18 floors	18	6	5	5	5	5	5	5	5	5
19 floors	19	6	5	5	5	5	5	5	5	5
20 floors	20	6	5	5	5	5	5	5	5	5
21 floors	21	6	5	5	5	5	5	5	5	5
22 floors	22	7	5	5	5	5	5	5	5	5
23 floors	23	7	5	5	5	5	5	5	5	5
24 floors	24	7	5	5	5	5	5	5	5	5
25 floors	25	7	5	5	5	5	5	5	5	5
30 floors	30	8	6	5	5	5	5	5	5	5
35 floors	35	8	6	6	6	6	6	6	6	6
40 floors	40	9	6	6	6	6	6	6	6	6
45 floors	45	9	7	6	6	6	6	6	6	6
50 floors	50	10	7	6	6	6	6	6	6	6
100 floors	100	14	9	8	7	7	7	7	7	7
200 floors	200	20	11	9	8	8	8	8	8	8
300 floors	300	24	13	10	9	9	9	9	9	9
400 floors	400	28	14	11	10	9	9	9	9	9
500 floors	500	32	15	11	10	10	9	9	9	9
1,000 floors	1000	45	19	13	11	11	11	10	10	10

A graphs is worth a thousand floors

Here’s the data plotted in graphical form. The y-axis represents the worst case number of drops needed to find the solution. The x-axis represents the number of floors in the building being tested (from 1 – 1000). There is a distinct line for each number of eggs.

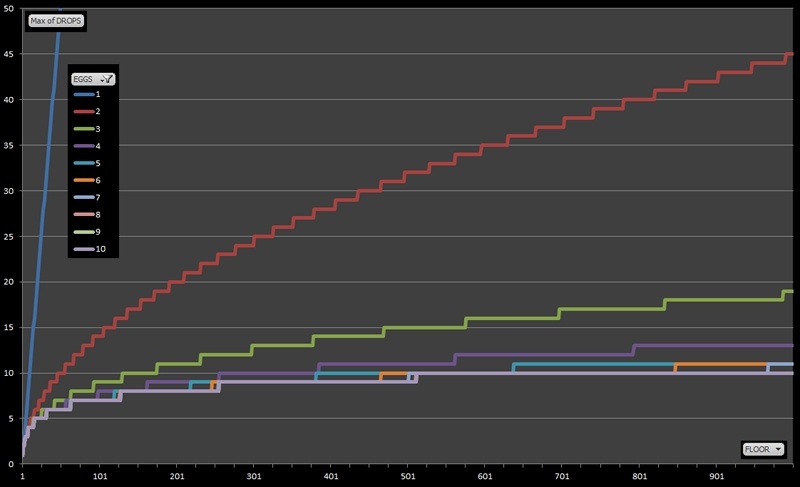
The blue line, representing the one egg solution, has a gradient of 1 and for every building, the worst case number of drops is the same as the number of floors.

Adding an extra egg to make two eggs makes a huge difference. Adding a third egg makes a smaller difference again.

For small numbers of floors and larger numbers of eggs, the solutions merge as we end up having excess eggs and the solution simplifies to that of the binary search as we discussed at the beginning of this article.

leetcode

egg-drop-with-2-eggs-and-n-floors | leetcode

给你 2 枚相同 的鸡蛋，和一栋从第 1 层到第 n 层共有 n 层楼的建筑。

已知存在楼层 f ，满足 0 <= f <= n ，任何从 高于 f 的楼层落下的鸡蛋都 会碎 ，从 f 楼层或比它低 的楼层落下的鸡蛋都 不会碎 。

每次操作，你可以取一枚 没有碎 的鸡蛋并把它从任一楼层 x 扔下（满足 1 <= x <= n）。如果鸡蛋碎了，你就不能再次使用它。如果某枚鸡蛋扔下后没有摔碎，则可以在之后的操作中 重复使用 这枚鸡蛋。

请你计算并返回要确定 f 确切的值 的 最小操作次数 是多少？

eg 1

输入：n = 2
输出：2

eg 2

输入：n = 100
输出：14

解:

dp[i][j] 表示有 i + 1 枚鸡蛋时，验证 j 层楼需要的最少操作次数， 我们可以分开分析 i = 0 和 i = 1 的情况：

i = 0 即只剩一枚鸡蛋，此时我们需要从 1 层开始逐层验证才能确保获取确切的 f 值，因此对于任意的 j 都有 dp[0][j] = j
i = 1，对于任意 j ，第一次操作可以选择在 [1, j] 范围内的任一楼层 k，如果鸡蛋在 k 层丢下后破碎，接下来问题转化成 i = 0 时验证 k - 1 层需要的次数，即 dp[0][k - 1], 总操作次数为 dp[0][k - 1] + 1； 如果鸡蛋在 k 层丢下后没碎，接下来问题转化成 i = 1 时验证 j - k 层需要的次数， 即 dp[1][j - k], 总操作次数为 dp[1][j - k] + 1，考虑最坏的情况，两者取最大值则有 dp[1][j] = min(dp[1][j], max(dp[0][k - 1] + 1, dp[1][j - k] + 1))

显然上面的 dp[0][j] 可以优化掉转为一维dp

func twoEggDrop(n int) int {
    dp := make([][]int, 2)
    for i := range dp {
        dp[i] = make([]int, n+1)
    }
    dp[1][0] = 0
    for j := 0; j < n+1; j++ {
        dp[0][j] = j
        dp[1][j] = j
    }
    for j := 1; j < n+1; j++ {
        for k := 1; k < j+1; k++ {
            dp[1][j] = util.Min(dp[1][j], util.Max(dp[0][k-1]+1, dp[1][j-k]+1))
        }
    }

    return dp[1][n]
}

func twoEggDropOpt(n int) int {
    // 显然上面的 dp[0][j] 可以优化掉转为一维dp
    dp := make([]int, n+1)
    for i := 0; i < n+1; i++ {
        dp[i] = n
    }
    dp[0] = 0
    for j := 1; j < n+1; j++ {
        for k := 1; k < j+1; k++ {
            dp[j] = util.Min(dp[j], util.Max(k, dp[j-k]+1))
        }
    }
    return dp[n]
}

super-egg-drop | leetcode

给你 k 枚相同的鸡蛋，并可以使用一栋从第 1 层到第 n 层共有 n 层楼的建筑。

已知存在楼层 f ，满足 0 <= f <= n ，任何从 高于 f 的楼层落下的鸡蛋都会碎，从 f 楼层或比它低的楼层落下的鸡蛋都不会破。

每次操作，你可以取一枚没有碎的鸡蛋并把它从任一楼层 x 扔下（满足 1 <= x <= n）。如果鸡蛋碎了，你就不能再次使用它。如果某枚鸡蛋扔下后没有摔碎，则可以在之后的操作中 重复使用 这枚鸡蛋。

请你计算并返回要确定 f 确切的值 的 最小操作次数 是多少？

示例 1：

输入：k = 1, n = 2
输出：2
解释：
鸡蛋从 1 楼掉落。如果它碎了，肯定能得出 f = 0 。
否则，鸡蛋从 2 楼掉落。如果它碎了，肯定能得出 f = 1 。
如果它没碎，那么肯定能得出 f = 2 。
因此，在最坏的情况下我们需要移动 2 次以确定 f 是多少。

示例 2：

输入：k = 2, n = 6
输出：3

示例 3：

输入：k = 3, n = 14
输出：4

解:

• k：有k个鸡蛋

• m：扔m次

• dp[k][m]：支持查找的最高楼层数——这个楼层数，可以通过用k个鸡蛋，扔m次，并保证找到鸡蛋不碎的最高楼层f。

原题：已知k个鸡蛋，n层楼，求最少扔多少次，一定能找到鸡蛋不碎的最高楼层f。
转化：已知k个鸡蛋，扔m次，最多支持多少层楼的查找，一定能找到鸡蛋不碎的最高楼层f。

你可以理解为一个从零开始拓展搜索边界的游戏——搜索楼层。dp[k][m]：支持查找的最高楼层数，就可以理解为：给定k、m，能搜索到的最大范围。

搜索过程：

第一步：
在大楼中的任意某一层开始首次搜索，占1层，消耗了1次搜索次数（扔鸡蛋次数m–）。
第二步：摔碎就下楼，没碎就上楼。
摔碎：下楼搜索之下部分。
没碎：上楼搜索之上部分。
我们知道dp[k][m]是支持查找的最高楼层数，对标着可以理解为最大的搜索范围，注意这里显然要包含所有可能被搜索到的范围。

我们知道： 总楼层数=之下楼层数+之上楼层数+1（本层）

要使搜索范围最大，则之下搜索范围、之上搜索范围都应该最大，即对应的dp值，所以可以建立状态转移方程如下：

dp[k][m] = dp[k][m - 1] + dp[k - 1][m - 1] + 1
按照上述的搜索流程，k个鸡蛋，扔m次，扔完第一次，可能上楼搜索，也可能下楼搜索。

没碎，上楼搜索的最大可能搜索范围为dp[k][m-1]。（k个鸡蛋，还能扔m-1次）
碎了，下楼搜索的最大可能搜索范围为dp[k-1][m-1]。（k-1个鸡蛋，还能扔m-1次）

func superEggDrop(k int, n int) int {
    dp := make([][]int, k+1)//k行n列（标号0不用）
    for i := range dp {
        dp[i] = make([]int, n+1)
    }
    // 构建dp
    m := 0
    for dp[k][m] < n {
        m++
        for i := 1; i <= k; i++ {
            dp[i][m] = dp[i][m-1] + dp[i-1][m-1] + 1
        }
    }
    return m
}