Golang data structure binary-tree

Herbert

2022-05-23

Golang

本文简单介绍数据结构中的树,主要介绍二叉树的基础并使用Go实现二叉树的创建及数组表示。

什么是树(Tree)?

树是一种抽象数据类型（ADT）或是实作这种抽象数据类型的数据结构，用来模拟具有树状结构性质的数据集合。它是由n（n>0）个有限节点组成一个具有层次关系的集合。把它叫做“树”是因为它看起来像一棵倒挂的树，也就是说它是根朝上，而叶朝下的。

如下图就是一棵树：

树不同于线性表中的链表、队列、栈，树结构是一种非线性存储结构，存储的是具有“一对多”关系的数据元素的集合。它具有以下的特点：

每个节点都只有有限个子节点或无子节点；
没有父节点的节点称为根节点；
每一个非根节点有且只有一个父节点；
除了根节点外，每个子节点可以分为多个不相交的子树；
树里面没有环路(cycle)；

树的术语

**节点的度(Degree)**：一个节点含有的子树的个数称为该节点的度；
**树的度(Degree of tree)**：一棵树中，最大的节点度称为树的度；
叶节点或终端节点：度为零的节点；
非终端节点或分支节点：度不为零的节点；
父亲节点或父节点：若一个节点含有子节点，则这个节点称为其子节点的父节点；
孩子节点或子节点：一个节点含有的子树的根节点称为该节点的子节点；
兄弟节点：具有相同父节点的节点互称为兄弟节点；
节点的层次：从根开始定义起，根为第1层，根的子节点为第2层，以此类推；
树的高度或深度：树中节点的最大层次；
堂兄弟节点：父节点在同一层的节点互为堂兄弟；
节点的祖先：从根到该节点所经分支上的所有节点；
**子孙(Descendant)**：以某节点为根的子树中任一节点都称为该节点的子孙。
**森林(Forest)**：由m（m>=0）棵互不相交的树的集合称为森林；

什么是二叉树(Binary Tree)？

二叉树是树类应用最广泛的一种数据结构，顾名思义，二叉树的每个节点最多只能包含两个孩子节点，一个节点可以包含0、1、2个孩子，如果是两个孩子，也就是通常我们说的左孩子和右孩子。

常见树分类

无序树：树中任意节点的子节点之间没有顺序关系，这种树称为无序树，也称为自由树。
有序树：树中任意节点的子节点之间有顺序关系，这种树称为有序树；
- 二叉树
  - 完全二叉树：二叉树中除去最后一层节点为满二叉树，且最后一层的节点依次从左到右分布；
  - 满二叉树：除了叶子节点，每个节点的度都为2；
  - 二叉搜索树(BST)
  - 平衡二叉树（AVL树）
- 霍夫曼树
- B树

二叉树的性质

经过前人的总结，二叉树具有以下几个性质：

二叉树中，第 i 层最多有 2i−1 个节点。
如果二叉树的深度为 K，那么此二叉树最多有 2K−1 个节点。
二叉树中，终端节点数（叶子节点数）为 n0，度为 2 的节点数为 n2，则 n0=n2+1。

下面证明第三点：

假设二叉树有N个节点,那么N = n0 + n1 + n2
从树的叶子节点到根节点思考，那么二叉树的边（两个节点的连接线）B = N - 1（除了根节点每个节点都有一条边）
从根节点到叶子节点思考，度为2的节点有两条变、度为1的节点有一条边、度为0的节点是叶子节点没有边，得到 B = 0n0 + 1n1 + 2*n2
因此我们得到 N - 1 = n1 + 2*n2
使用n0 + n1 + n2 替换N，得到 n0 + n1 + n2 - 1 = n1 + 2*n2
得到n0=n2+1

二叉树的存储结构

顺序存储

指的是使用顺序表（数组）存储二叉树。需要注意的是，顺序存储只适用于完全二叉树。换句话说，只有完全二叉树才可以使用顺序表存储。因此，如果我们想顺序存储普通二叉树，需要提前将普通二叉树转化为完全二叉树

链式存储

二叉树并不适合用数组存储，因为并不是每个二叉树都是完全二叉树，普通二叉树使用顺序表存储或多或多会存在空间浪费的现象

二叉树的数组表示

为了方便描述一个二叉树，我们使用数组表示，如果是普通二叉树我们先转化成完全二叉树，为空的节点可以约定一个值（比如NULL）来表示，我们从树的根节点开始按从底层到高层从左到右的顺序依次排列节点。

示例：

转化成完全二叉树后：

完全二叉树

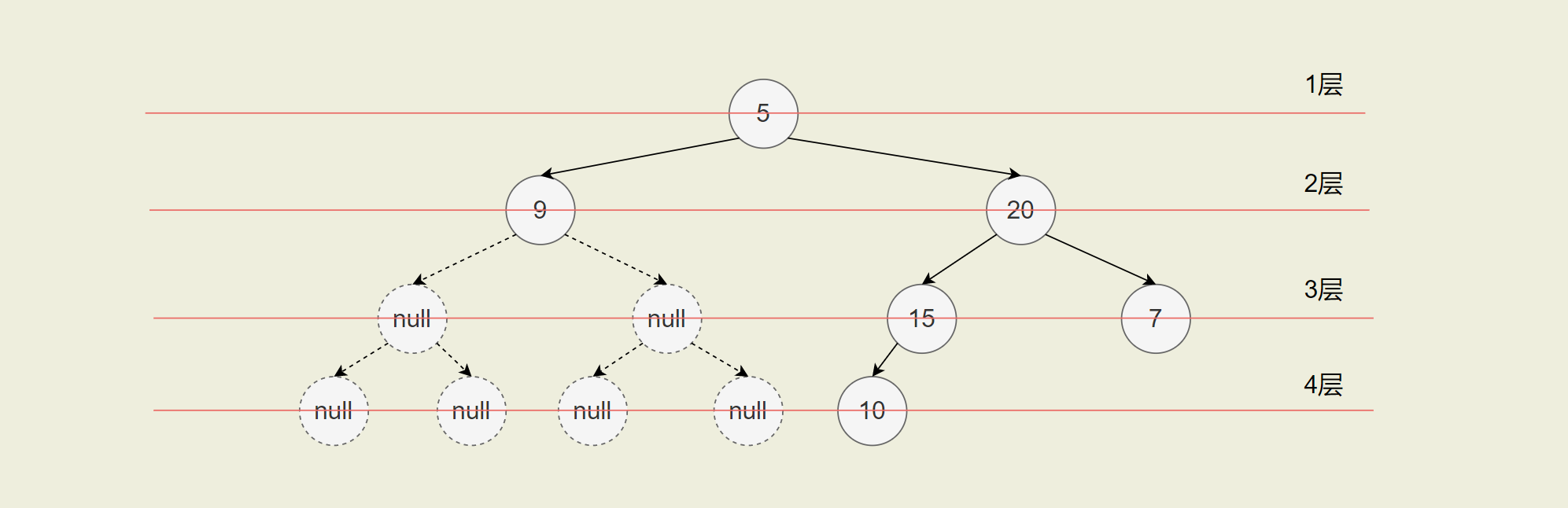
最终得到数组：[5,9,20,null,null,15,7,null,null,null,null,10]

假设某个节点索引值为index（根节点为0），那么节点索引之间满足以下算式：

左子节点索引：2*index+1
右子节点索引为：2*index+2
父节点索引为：(index-1)/2

基于以上的数组表示法，我们构造一个函数BuildTree，输入数组得到一棵二叉树并返回根节点，使用0表示空节点：

tree.go

package tree

type Node struct {
  Val         int
  Left, Right *Node
}

// BuildTree 输入一个切片 ：[3,9,20,0,0,15,7]
func BuildTree(l []int) (root *Node) {
  length := len(l)
  if length == 0 {
    return root
  }

  var nodes = make([]*Node, length)
  root = &Node{
    Val: l[0],
  }
  nodes[0] = root
  //循环输入的数组切片，依次判断每一个节点的左右节点是否存在并创建
  for i := 0; i < length; i++ {
    currentNode := nodes[i]

    if currentNode == nil {
      continue
    }

    leftIndex := 2*i + 1
    if leftIndex < length && l[leftIndex] != 0 {
      currentNode.Left = &Node{
        Val: l[leftIndex],
      }
      nodes[leftIndex] = currentNode.Left
    }

    rightIndex := 2*i + 2
    if rightIndex < length && l[rightIndex] != 0 {
      currentNode.Right = &Node{
        Val: l[rightIndex],
      }
      nodes[rightIndex] = currentNode.Right
    }
  }

  return root
}

这样创建一棵二叉树：

root := tree.BuildTree([]int{3, 9, 20, 0, 0, 15, 7})

树转化成数组

上面我们使用BuildTree函数从数组创建了一棵树，那么我们下面再写一个函数ConvertToArr做一个逆运算将一棵树转化成数组来表示，先看代码：

// ConvertToArr 树转化成数组
func ConvertToArr(root *Node) []int {
    if root == nil {
        return []int{}
    }

    result := indexRecursion(root, 1, 0, []int{})
    // 删除末尾的0
    for i := len(result) - 1; i >= 0; i-- {
        if result[i] == 0 {
            result = result[:i]
        } else {
            break
        }
    }

    return result
}

// 索引循环
func indexRecursion(node *Node, level int, index int, result []int) []int {
    //深度为level的树最多有2^level-1个节点，容量不够时扩容依据
    if len(result) < (1<<level - 1) {
        newArr := make([]int, 1<<level-1)
        copy(newArr, result)
        result = newArr
    }
    result[index] = node.Val

    if node.Left != nil {
        result = indexRecursion(node.Left, level+1, 2*index+1, result)
    }

    if node.Right != nil {
        result = indexRecursion(node.Right, level+1, 2*index+2, result)
    }

    return result
}

尝试转化一棵树：

root := tree.BuildTree([]int{5, 9, 20, 0, 22, 15, 7, 0, 0, 0, 0, 10, 30})
result := tree.ConvertToArr(root)
fmt.Println(result)

输出：

[5 9 20 0 22 15 7 0 0 0 0 10 30]

上面代码中level表示层次，然后索引从0开始，所以根节点的level=1，index=0 ConvertToArr函数是对二叉树的性质及二叉树数组索引算式的应用。

如何获取二叉树最大深度?

回忆下概念：树的深度指的是树中最大的节点层。

这是一道力扣算法题 104.二叉树的最大深度

对于二叉树：

下面给出两种计算方式：

深度优先搜索（DFS）

访问的顺序是：1->2->4->3->5->6

dfsRecursion函数返回的切片是一个按层来排列节点的二维切片，例：[1,[2,3],[4,5,6]]

// MaxDepth 计算树的深度
func MaxDepth(root *Node) int {
    return len(dfsRecursion(root, 0, [][]int{}))
}

// 深度优先
func dfsRecursion(node *Node, level int, nodes [][]int) [][]int {
    if node == nil {
        return nodes
    }
    // 判断切片长度是否满足要求
    if level < len(nodes) {
        nodes[level] = append(nodes[level], node.Val)
    } else {
        nodes = append(nodes, []int{node.Val})
    }
    nodes = dfsRecursion(node.Left, level+1, nodes)
    nodes = dfsRecursion(node.Right, level+1, nodes)

    return nodes
}

DFS 深度搜索-从上到下

type TreeNode struct {
    Val   int
    Left  *TreeNode
    Right *TreeNode
}

func preorderTraversal(root *TreeNode) []int {
    result := make([]int, 0)
    dfs(root, &result)
    return result
}

// V1：深度遍历，结果指针作为参数传入到函数内部
func dfs(root *TreeNode, result *[]int) {
    if root == nil {
        return
    }
    *result = append(*result, root.Val)
    dfs(root.Left, result)
    dfs(root.Right, result)
}

DFS 深度搜索-从下向上（分治法）

// V2：通过分治法遍历
func preorderTraversal(root *TreeNode) []int {
    result := divideAndConquer(root)
    return result
}
func divideAndConquer(root *TreeNode) []int {
    result := make([]int, 0)
    // 返回条件(null & leaf)
    if root == nil {
        return result
    }
    // 分治(Divide)
    left := divideAndConquer(root.Left)
    right := divideAndConquer(root.Right)
    // 合并结果(Conquer)
    result = append(result, root.Val)
    result = append(result, left...)
    result = append(result, right...)
    return result
}

注意点：

DFS 深度搜索（从上到下）和分治法区别：前者一般将最终结果通过指针参数传入，后者一般递归返回结果最后合并

宽度优先搜索（BFS）

宽度优先就是从上到下，先把每一层遍历完之后再遍历一下一层。

访问的顺序是：1->2->3->4->5->6

使用一个Queue，将root节点初始化进队列，然后依次插入节点到头部，从尾部消耗节点的方式来完成BFS。

代码如下：

func BFS(root *Node) [][]int {
    // 通过上一层的长度确定下一层的元素
    result := make([][]int, 0)
    if root == nil {
        return result
    }
    queue := make([]*Node, 0)
    queue = append(queue, root)
    for len(queue) > 0 {
        list := make([]int, 0)
        // 为什么要取length？
        // 记录当前层有多少元素（遍历当前层，再添加下一层）
        l := len(queue)
        for i := 0; i < l; i++ {
            // 出队列
            level := queue[0]
            queue = queue[1:]
            list = append(list, level.Val)
            if level.Left != nil {
                queue = append(queue, level.Left)
            }
            if level.Right != nil {
                queue = append(queue, level.Right)
            }
        }
        result = append(result, list)
    }
    return result
}

分治法应用

先分别处理局部，再合并结果

适用场景

快速排序
归并排序
二叉树相关问题

分治法模板

递归返回条件
分段处理
合并结果

func traversal(root *TreeNode) ResultType  {
    // nil or leaf
    if root == nil {
        // do something and return
    }

    // Divide
    ResultType left = traversal(root.Left)
    ResultType right = traversal(root.Right)

    // Conquer
    ResultType result = Merge from left and right

    return result
}

范例

分治法遍历二叉树

// V2：通过分治法遍历二叉树
func preorderTraversal(root *TreeNode) []int {
    result := divideAndConquer(root)
    return result
}
func divideAndConquer(root *TreeNode) []int {
    result := make([]int, 0)
    // 返回条件(null & leaf)
    if root == nil {
        return result
    }
    // 分治(Divide)
    left := divideAndConquer(root.Left)
    right := divideAndConquer(root.Right)
    // 合并结果(Conquer)
    result = append(result, root.Val)
    result = append(result, left...)
    result = append(result, right...)
    return result
}

归并排序

func MergeSort(nums []int) []int {
    return mergeSort(nums)
}
func mergeSort(nums []int) []int {
    if len(nums) <= 1 {
        return nums
    }
    // 分治法：divide 分为两段
    mid := len(nums) / 2
    left := mergeSort(nums[:mid])
    right := mergeSort(nums[mid:])
    // 合并两段数据
    result := merge(left, right)
    return result
}
func merge(left, right []int) (result []int) {
    // 两边数组合并游标
    l := 0
    r := 0
    // 注意不能越界
    for l < len(left) && r < len(right) {
        // 谁小合并谁
        if left[l] > right[r] {
            result = append(result, right[r])
            r++
        } else {
            result = append(result, left[l])
            l++
        }
    }
    // 剩余部分合并
    result = append(result, left[l:]...)
    result = append(result, right[r:]...)
    return
}

递归需要返回结果用于合并

快速排序

func QuickSort(nums []int) []int {
    // 思路：把一个数组分为左右两段，左段小于右段，类似分治法没有合并过程
    quickSort(nums, 0, len(nums)-1)
    return nums

}
// 原地交换，所以传入交换索引
func quickSort(nums []int, start, end int) {
    if start < end {
        // 分治法：divide
        pivot := partition(nums, start, end)
        quickSort(nums, 0, pivot-1)
        quickSort(nums, pivot+1, end)
    }
}
// 分区
func partition(nums []int, start, end int) int {
    p := nums[end]
    i := start
    for j := start; j < end; j++ {
        if nums[j] < p {
            swap(nums, i, j)
            i++
        }
    }
    // 把中间的值换为用于比较的基准值
    swap(nums, i, end)
    return i
}
func swap(nums []int, i, j int) {
    t := nums[i]
    nums[i] = nums[j]
    nums[j] = t
}

快排由于是原地交换所以没有合并过程传入的索引是存在的索引（如：0、length-1 等），越界可能导致崩溃

常见题目

给定一个二叉树，找出其最大深度 maximum-depth-of-binary-tree

给定一个二叉树，判断它是否是高度平衡的二叉树 balanced-binary-tree

给定一个非空二叉树，返回其最大路径和 binary-tree-maximum-path-sum

给定一个二叉树, 找到该树中两个指定节点的最近公共祖先 lowest-common-ancestor-of-a-binary-tree