IQ Interview Question
掷两次骰子
掷骰子,游戏规则:希望结果尽可能大,如果对第一次的结果不满意可以掷第二次,但是第一次结果就作废了,以第二次的结果为准。这个掷骰子结果的数学期望是多少呢?
掷一次:
1 * 1/6 + 2 * 1/6 + … + 6 * 1/6 = 3.5
如果第一次扔到1,2,3是要扔第二次的,4,5,6则不需要。
5 * 1/2 + 3.5 * 1/2 = 4.25
一个木棍分三段组成三角形
作图 x,y 横轴纵轴,中间的小三角
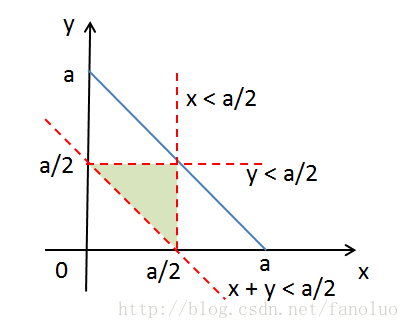
1/4
扔硬币,先到正面的赢,先手赢的概率
先手赢的概率为p,这个p由两个部分组成,第一个是第一次就正面,概率是1/2。第二种情况是第一次没有投到正面,此时轮到后手了,从这个时候看就变成相当于后手为第一轮了,那么当然同样的后手赢的概率也为p,但是只能有一个先吃,所以这里先手赢的概率就是 1 - p,那么完整的式子就是:p = 1/2 + 1/2(1-p),求解出来 p也是 2/3
三扇关闭的门,汽车和羊
有三扇关闭的门,其中一扇门后面有一辆汽车,而另外两扇门后面各有一只山羊。一个人被要求选择一扇门,他会赢得这扇门后面的奖品。在选定一扇门之后,主持人打开剩下两扇门中的一扇,露出一只山羊。主持人知道每扇门后面有什么,不会打开那扇门后面有汽车的门。现在,这个人可以选择改变他的选择,选择另一扇未被打开的门,或者保持原先的选择。那么,这个人改变他的选择会增加他获得汽车的概率吗?
会增加,因为只要一开始选到羊, 换了就会得到汽车这个概率是2/3,直接选汽车的概率是1/3 即改变前:1/3 改变后:2/3
100层楼玻璃球
有一栋100层高的大楼,给你两个完全相同的玻璃球。假设从某一层开始,丢下玻璃球会摔碎。那么怎么利用手中的两个球,用什么最优策略知道这个临界的层是第几层?
第一种方案
先从第 10 楼扔,再从第 20 楼扔,依次下去。发现如果是11层,需要试11次,如果是99层需要试19次,不稳定,需要考虑最坏的情况
第二种方案
假设最少尝试次数为 x ,那么,第一个杯子必须要从第 x 层扔下,因为:如果碎了,前面还有 x - 1 层楼可以尝试,如果没碎,后面还有 x-1 次机会。
如果没碎,第一个杯子,第二次就可以从 x +(x - 1)层进行尝试,这里加上 x - 1,是因为当此时,第一个杯子碎了,第二个杯子还有可以从 x + 1 到 ( x + (x - 1) - 1 ) 层进行尝试,有 x - 2 次机会。
如果还没碎,那第一个杯子,第三次从 x + (x - 1) + (x - 2)层尝试。不管杯子碎或者没碎,都有 x - 3 次尝试机会,依次类推。
那么经过 x 次的尝试可以确定最高的楼层为 x + (x - 1) + (x - 2) + … + 1 = x(x+1) / 2 >= 100
解得n = 13.65。最少要尝试 14 次。
有20%蓝车,80%绿车,有车肇事,目击者称看见蓝车,专家说能看见正确的车的概率是80%,问肇事蓝车的概率
有两种情况导致最后看到是蓝车:
真的是蓝车,而且看对了 20% * 80%
其实是绿车,看错了 80% * 20%
$\frac{20% × 80%}{20% × 80% + 80% × 20%} = 50%$
50个红球和50个篮球,放入两个箱子,怎么样放置才能使拿到红球的概率最大
一个罐子1个红球 ,另一个罐子49个红球,50个蓝球
赛马问题,25匹马,5赛道,取前三名
首先比5次,
A1 A2 A3 A4 A5
B1 B2 B3 B4 B5
C1 C2 C3 C4 C5
D1 D2 D3 D4 D5
E1 E2 E3 E4 E5
第6次,假设结果是
A1 B1 C1 D1 E1
25中的第一一定是A1,
第二名只有可能是 A2 B1
第三名只有可能是 A2 B1 A3 B2 C1
第7次比赛
A2 B1 A3 B2 C1 一起比,第2,3名同时产生
100个人回答五道题
有81人答对第一题,91人答对第二题,85人答对第三题,79人答对第四题,74人答对第五题。答对三道题或三道题以上的人算及格,那么在这100人中至少有多少人及格呢?
至少多少人及格 -> 最多多少人不及格 -> 要想不及格的人尽可能多,就要平均每个人错的题尽可能少,而且要不及格,那最少就错3题。
每道题的答错人数为:26,21,19,15,9
加起来是 90 . 90 / 3 = 30最多30人不及格。至少70人及格
注意:19,9,15,21,26这个序列,真的可以正好被30个人平分,每人错3题吗?可以
怎样的序列才能恰好被平分,每人错3题呢?
首先,序列的和,必须是3的倍数。然后,通过模拟分配过程可以发现,只需要每次找出序列中最大的三项,然后这三项每一项都减1,记录为1次操作,如此迭代,直到无法找出不为0的三项为止。最后统计操作次数,就可以得出这个序列最多能被平分给多少人。
迭代完成后,如果不能被平分,那么剩下的序列的情况只有两种:X,0,0,0,0 或X,Y,0,0,0。我们可以发现,只需要存在(a+b+c+d)/2<X 或 (a+b+c)*2<(X+Y),就不能被正好平分。所以只要验证下最小的4个数的和除以2是不是比最大的数小,或者最小的三个数的和乘以2是不是小于最大的两个数的和,就可以判断出来能不能正好平分了。
根据这个条件,可以举出反例:5,5,5,12,15 。
抛硬币次数的期望
持续抛1枚硬币,直到连续出现2次正面为止,求扔的期望次数
假设平均抛 x 次结束游戏。
如果第一次抛的是0,那么再抛x次就能结束游戏(因为第一个0对后面抛的没有影响),共抛x+1次;
如果第一次抛的是’1’,那么头两次抛有两种情况,’11’和’10’:
抛出’11’已经结束游戏,一共抛2次;
抛出’10’则还需要抛x次才能结束(因为第2次抛出’0’相当于把前面的结果清空了),一共抛x+2次。
这样可以列出:x = 0.5(x+1) + 0.25 * 2 + 0.25 * (x+2)
解出 x = 6.
https://www.zybuluo.com/zsh-o/note/1175045
https://www.cnblogs.com/avril/p/3161669.html
http://www.matrix67.com/blog/archives/3638
如果直到连续出现n次正面为止,